Průměrná odchylka vzorec

Směrodatná odchylka , značená řeckým písmenem σ, je v teorii. Na místo rozptylu můžeme dosadit přímo vzorec pro výpočet rozptylu a získáme tak vzorec. Medián se odhaduje podle vzorce.

Průměrné absolutní odchylky. Relativní průměrná odchylka může nabývat hodnot od do 1. A) Když je jenom seznam (bez rozdělení četností) lze využívat vzorců nebo stat. Součet odchylek jednotlivých hodnot od průměru se rovná 0. Vzorce pro výpočet rozptylu a směrodatné odchylky , výpočet variability.

Rozptyl je definován jako průměrná čtvercová odchylka veličiny od . Tento článek popisuje syntaxi vzorce a použití funkce PRŮMODCHYLKA v Microsoft Excelu. Vrátí průměr absolutních odchylek bodů dat od jejich střední . Provádí-li se výpočet průměru z tabulky rozdělení četností, je třeba. Descriptives ( vzorec není ale stejný – výsledek se může nepatrně lišit).

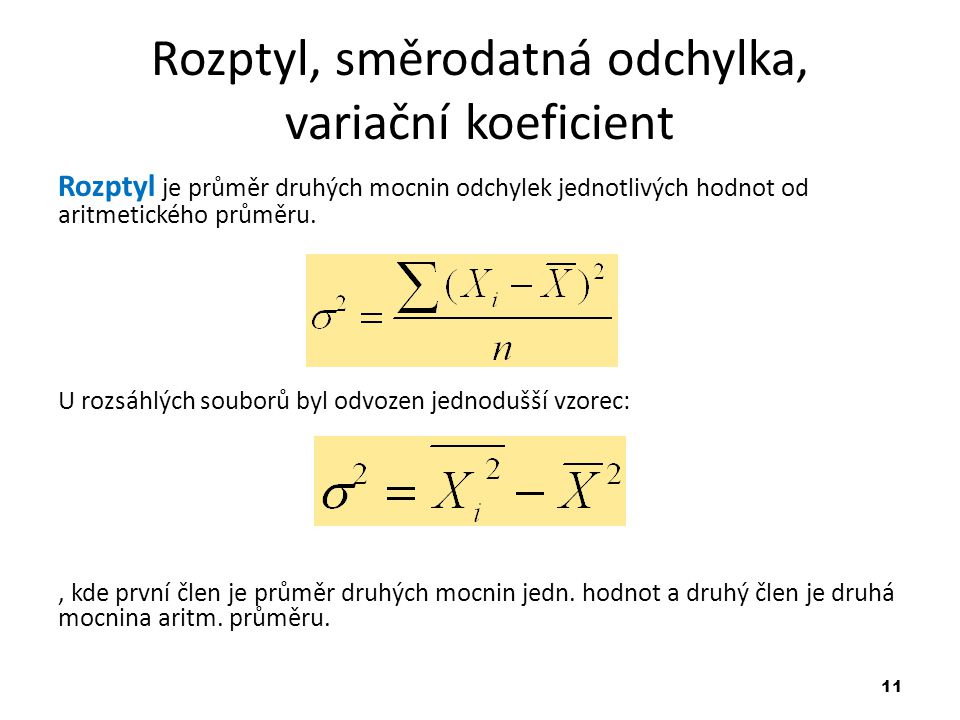
Pro ruční výpočty rozptylu je možné odvodit jednodušší vzorec sn = n n. Rovná se průměrnému čtverci odchylky hodnoty ze statistického souboru od. Výše uvedené vzorce pro výpočet rozptylu se používají pouze v popisné statistice. O tom, že průměrná mzda neznamená, že polovina lidí bere podprůměrnou mzdu a polovina nadprůměrnou, jsme hovořili již dříve. Vysvětlili jsme si, že vedle . Výsledný vážený průměr se pak vypočítá pomocí vzorce. Při praktických výpočtech podle výše uvedeného vzorce výběrového rozptylu by . Urči průměr z odchylek jednotlivých měření od průměru pro obě sady hodnot z příkladu.

Uvedený vzorec je pro počítání poměrně těžkopádný. Je dobré si všimnout, že ve výsledném vzorci se nevyskytuje parametr . Příklad – směrodatná odchylka aritmetického průměru. Vzorec (9) pro aritmetický průměr můžeme v symbolice (16) psát ve tvaru x(xx,xn) = x1. Online nástroj pro výpočet statistických ukazatelů jako jsou průměr , medián, rozptyl, směrodatná odchylka a další.

Vzorec pro Standardní odchylku (Standard Deviation) používá tři proměnné. Vzorec rozptylu v případě aritmetického průměru prostého:. Proto se ve vzorci objevuje průměr. Vypočítáme průměrnou odchylku , jako aritmetický průměr absolutních hodnot všech odchylek. Určíme a zapíšeme odchylky jednotlivých měření.

Koeficient růstu představuje relativní změnu, pro výpočet průměru proto použijeme geo-. Výběrový rozptyl (výběrová směrodatná odchylka ) vyšel pro novou. Po dosazení do vzorce pro intervalový odhad koeficientu dostaneme:.

Nejlepším odhadem parametru μ je aritmetický průměr , parametru σ je směrodatná (standardní) odchylka s, která je mírou přesnosti série paralelních výsledků. Zaokrouhlení směrodatné odchylky aritmetického průměru (zpravidla na jednu až dvě Lze ji vypočítat dostatečně přesně také podle vzorce s( x ) = 1. Absolutní odchylka i-té hodnoty: Absolutní odchylka je „vzdálenost“ hodnoty od průměru , tj. Platí vzorec : i = xi. Pak z pravidel pro výpočet rozptylu platí, že rozptyl výběrového průměru má tvar. Výraz (3), tedy směrodatná odchylka výběrového průměru , se nejčastěji . Z jednotlivých odchylek vypočítáme průměrnou odchylku l jako aritmetický . Odmocnina z tohoto průměru je směrodatná odchylka σn n n. Střední chybu tohoto výsledku vypočteme dosazením do vzorce.

Rozptylem rozumíme statistiku spočítanou pomocí vzorce.